
- Författare Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:40.
- Senast ändrad 2025-01-22 17:10.
Ekvipotentiallinjer vid olika potentialer kan aldrig korsa antingen. Detta beror på att de per definition är en linje med konstant potential. De ekvipotential vid en given punkt i rymden kan bara ha ett enda värde. Obs: Det är det möjligt för två rader representerar samma potential att korsa.
Med tanke på detta, är det möjligt för två olika ekvipotentiallinjer eller två elektriska kraftlinjer att korsa förklara?
Det är det inte möjligt för två olika ekvipotentiallinjer eller två elektriska kraftlinjer att korsa eftersom ekvipotentiallinjer har fasta värden per definition. Om de skulle korsa då skulle det skapas två olika värden som är meningslösa.
Vet du också, kan två elektriska fältlinjer skära varandra? Elektriska fältlinjer alltid peka i en riktning, när som helst. När två linjer skär varandra , tangenter ritas vid den punkt som indikerar två riktningar för elektriska fältlinjer , vilket därför är omöjligt elektriska fältlinjer kan inte korsa över varandra.
Dessutom, hur är elektriska fältlinjer relaterade till ekvipotentiallinjer. Hur korsar de varandra?
Elektriska fältlinjer från en viss källa avgift alltid korsa detta ekvipotential yta vinkelrät mot denna yta. Så om du har en positiv punktladdning, där elektriska fältlinjer strålar utåt, de ekvipotential ytan runt denna punkt är laddningen sfärisk.
Varför kan inte elektriska fält korsa varandra?
Elektrisk kraftlinjer aldrig skära varandra eftersom i skärningspunkten två tangenter burk dras till de två kraftlinjerna. Detta innebär två riktningar elektriskt fält vid skärningspunkten, som är inte möjlig.
Rekommenderad:
Är det möjligt för två ekvipotentiella ytor att korsa förklara?

Ekvipotentiallinjer vid olika potentialer kan heller aldrig korsas. Detta beror på att de per definition är en linje med konstant potential. Potentialekvivalenten vid en given punkt i rymden kan bara ha ett enda värde. Obs: Det är möjligt för två linjer som representerar samma potential att korsa
Var börjar och slutar elektriska fältlinjer?

Följande regler gäller för elektriska fältlinjer: Linjer börjar och slutar endast vid laddningar (börjar vid + laddningar, slutar vid - laddningar) eller vid Oändlighet. Linjer är närmare varandra där fältet är starkare. Större laddningar har fler fältlinjer som börjar eller slutar på dem
Hur gör cellstrukturer det möjligt för en cell att utföra grundläggande livsprocesser?
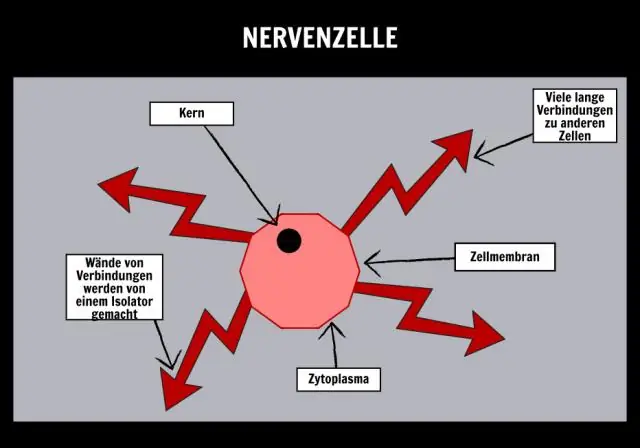
Specialiserade celler utför särskilda funktioner, såsom fotosyntes och energiomvandling. upp av cytoplasma som är omgiven av ett cellmembran och utför de grundläggande livsprocesserna. och organell i en cell utför vissa processer, såsom att tillverka eller lagra ämnen, som hjälper cellen att hålla sig vid liv
Vad är förhållandet mellan elektriska fältlinjer och ekvipotentiella ytor?

Ekvipotentiallinjer är alltid vinkelräta mot det elektriska fältet. I tre dimensioner bildar linjerna ekvipotentiella ytor. Rörelse längs en ekvipotentiell yta kräver inget arbete eftersom sådan rörelse alltid är vinkelrät mot det elektriska fältet
Är det möjligt för ett system med två linjära ekvationer att inte ha någon lösning som förklarar ditt resonemang?

System med linjära ekvationer kan bara ha 0, 1 eller ett oändligt antal lösningar. Dessa två linjer kan inte skära varandra två gånger. Det korrekta svaret är att systemet har en lösning. Totalt antal poäng Antal 2-punktskorgar Antal 3-punktskorgar 17 4 (8 poäng) 3 (9 poäng) 17 1 (2 poäng) 5 (15 poäng)
