Video: Vad är derivatan COS X?
2024 Författare: Miles Stephen | [email protected]. Senast ändrad: 2023-12-15 23:41
Med hjälp av det faktum att derivat av synd ( x ) är cos ( x ), använder vi visuella hjälpmedel för att visa att derivat av cos ( x ) är -synd( x ).
Därefter kan man också fråga sig, vad är derivatan av negativ Cos X?
Därför derivata av f(x)=− synd (x) är f'(x)=−cos(x).
vad är derivatan av 1? De Derivat talar om för oss lutningen för en funktion vid vilken punkt som helst. Det finns regler vi kan följa för att hitta många derivat . Till exempel: Lutningen för ett konstant värde (som 3) är alltid 0.
Derivat Regler.
| Vanliga funktioner | Fungera | Derivat |
|---|---|---|
| Konstant | c | 0 |
| Linje | x | 1 |
| yxa | a | |
| Fyrkant | x2 | 2x |
På samma sätt, vad är derivatan av Cos Square x?
De derivata av cos ( x ) är -synd( x ). De derivat av 2x är 2.
Varför är derivat av synd cos?
Det beror på att funktionen cos (x) råkar beskriva beteendet hos lutningen av tangentlinjerna för synd (x) för varje x. Detta är definitionen av a derivat . Därav synd cos är också relaterade. Och relaterade saker kan härledas.
Rekommenderad:
Vad är Sin Cos Tan-formeln?
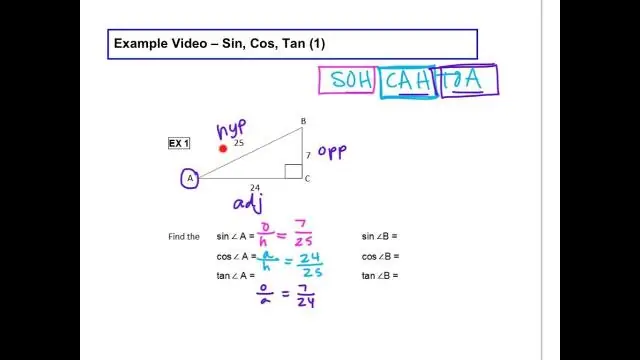
Funktionerna för sin, cos och tan kan beräknas enligt följande: Sinus Funktion:sin(θ) = Motsatt / Hypotenus. CosineFunction: cos(θ) = Adjacent / Hypotenuse.Tangent Funktion: tan(θ) = Motsatt /Angränsande
Vad är derivatan av Sinh 2x?
Derivatan av sinh(u) sinh (u) med avseende på u u är cosh(u) cosh (u). Ersätt alla förekomster av u u med 2x 2x
Vad är derivatan av en kvot?
KVOTIENTREGEL I ord kan man komma ihåg detta som: 'Derivatan av en kvot är lika med botten gånger derivatan av toppen minus toppen gånger derivatan av botten, dividerat med botten i kvadrat.'
Vad är derivatan av Secx 2?
Vi vet att derivatan av g(x) = sec x är g'(x) = secx tanx, så vi multiplicerar 2sec x med secx tanx för att få vårt svar. Vi ser att derivatan av sek 2 x är 2 sek 2 x tan x
Vad är derivatan av rörelsemängd?
Nyckelekvationer Hastigheten för masscentrum för rullande föremål vCM=Rω Derivata av rörelsemängd är lika med vridmoment d→ldt=∑→τ Vinkelmomentet för ett system av partiklar →L=→l1+→l2+⋯+→lN För ett system av partiklar är derivatan av vinkelmomentet lika med vridmomentet d→Ldt=∑→τ Vinkelmoment hos en roterande stel kropp L=Iω