
- Författare Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:40.
- Senast ändrad 2025-01-22 17:10.
I matematik, a grupp är en uppsättning utrustad med en binär operation som kombinerar två valfria element för att bilda ett tredje element på ett sådant sätt att fyra villkor kallas grupp axiom är uppfyllda, nämligen stängning, associativitet, identitet och inverterbarhet. Grupper delar ett grundläggande släktskap med begreppet symmetri.
Vad är gruppen och dess egenskaper i detta avseende?
A grupp är en ändlig eller oändlig uppsättning element tillsammans med en binär operation (kallad grupp operation) som tillsammans uppfyller de fyra grundläggande egenskaper av stängning, associativitet, identiteten fast egendom , och det omvända fast egendom.
För det andra, vad är grupper i abstrakt algebra? Definition. A grupp (G, ·) är en icke-tom mängd G tillsammans med en binär operation · på G så att följande villkor gäller: (i) Stängning: För alla a, b G är elementet a · b ett unikt definierat element av G. (ii) Associativitet: För alla a, b, c G, vi har. a · (b · c) = (a · b) · c.
Också att veta, VAD ÄR grupp i linjär algebra?
I matematik, a linjär algebraisk grupp är en undergrupp till grupp av inverterbara n×n-matriser (under matris multiplikation) som definieras av polynomekvationer. Många ljuger grupper kan ses som linjära algebraiska grupper över fältet av reella eller komplexa tal.
Vad gör en grupp till en grupp?
A grupp är en samling individer som har relationer till varandra som gör dem beroende av varandra i någon betydande grad. Som så definierat, termen grupp hänvisar till en klass av sociala enheter som har den gemensamma egenskapen att det är ömsesidigt beroende mellan sina ingående medlemmar.
Rekommenderad:
Vad är en homogen grupp?

Homogen gruppering är placeringen av elever med liknande förmågor i ett klassrum. Alla begåvade barn inom samma årskurs kommer att gå i samma klassrum. Termen syftar oftare på elever med funktionsnedsättning snarare än elever som är begåvade eller avancerade
Vad kallas en grupp celler?
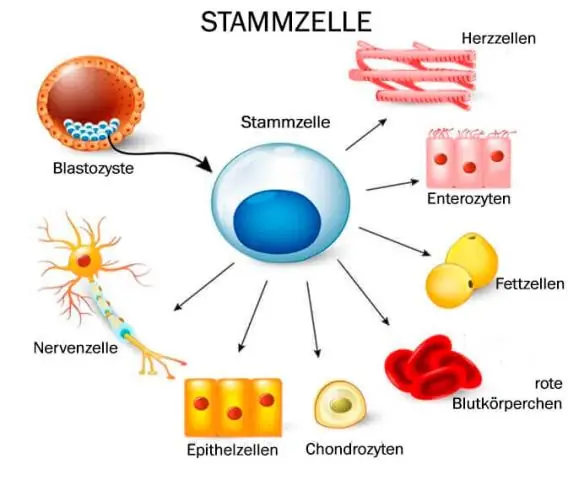
En grupp av specialiserade celler kallas vävnad
Vad är definitionen av en grupp i det periodiska systemet?

Inom kemi är en grupp (även känd som en familj) en kolumn av element i det periodiska systemet för de kemiska elementen. Det finns 18 numrerade grupper i det periodiska systemet; f-blockets kolumner (mellan grupperna 3 och 4) är inte numrerade
Vad är skillnaden mellan Algebra 1 och Algebra 2?

Det primära fokus för Algebra 1 är att lösa ekvationer. De enda funktionerna du kommer att titta på utförligt är linjära och kvadratiska. Algebra 2 är mycket mer avancerat
VAD ÄR grupp i linjär algebra?

En grupp är en finit eller oändlig uppsättning element tillsammans med en binär operation (kallad gruppoperation) som tillsammans uppfyller de fyra grundläggande egenskaperna stängning, associativitet, identitetsegenskapen och den inversa egenskapen
