Innehållsförteckning:
Video: Kan vi utföra regression på icke-linjära data?
2024 Författare: Miles Stephen | [email protected]. Senast ändrad: 2023-12-15 23:40
Icke-linjär regression kan passar många fler typer av kurvor, men det burk kräver mer ansträngning både för att hitta den bästa passformen och att tolka de oberoende variablernas roll. Dessutom är R-kvadrat inte giltigt för icke-linjär regression , och det är omöjligt att Beräkna p-värden för parameteruppskattningarna.
På så sätt kan en regression vara olinjär?
I statistiken, icke-linjär regression är en form av regression analys där observationsdata modelleras av en funktion som är en olinjär kombination av modellparametrarna och beror på en eller flera oberoende variabler. Data anpassas med en metod för successiva approximationer.
Man kan också fråga sig, är r kvadrerat endast för linjär regression? Den allmänna matematiska ramen för R - kvadrat fungerar inte korrekt om regressionsmodell är inte linjär . Trots detta problem räknar de flesta statistiska program fortfarande R - kvadrat för icke-linjära modeller. Om du använder R - kvadrat att välja det bästa modell , det leder till det riktiga endast modell 28-43% av tiden.
Angående detta, hur beräknar man icke-linjär regression?
Om din modell använder en ekvation i formen Y = a0 + b1X1, det är en linjär regression modell. Om inte, så är det olinjär.
Y = f(X, β) + e
- X = en vektor av p-prediktorer,
- β = en vektor med k parametrar,
- f(-) = en känd regressionsfunktion,
- ε = en felterm.
Vilka typer av regression finns det?
Typer av regression
- Linjär regression. Det är den enklaste formen av regression.
- Polynomregression. Det är en teknik för att anpassa en olinjär ekvation genom att ta polynomfunktioner av oberoende variabel.
- Logistisk tillbakagång.
- Kvantilregression.
- Ridge regression.
- Lasso regression.
- Elastisk nätregression.
- Principal Components Regression (PCR)
Rekommenderad:
Vilka organismer kan utföra fotosyntes och cellandning?
Växter som utsätts för ljus kommer att utföra både fotosyntes och cellandning. Efter en tid i mörkret kommer endast cellandning att förekomma i växterna. Under fotosyntesen avger växter syre. Under cellandning avger växter koldioxid
Hur beräknar man icke-linjär regression?
Om din modell använder en ekvation i formen Y = a0 + b1X1, är det en linjär regressionsmodell. Om inte är det olinjärt. Y = f(X,β) + ε X = en vektor av p-prediktorer, β = en vektor med k parametrar, f(-) = en känd regressionsfunktion, ε = en felterm
Hur gör cellstrukturer det möjligt för en cell att utföra grundläggande livsprocesser?
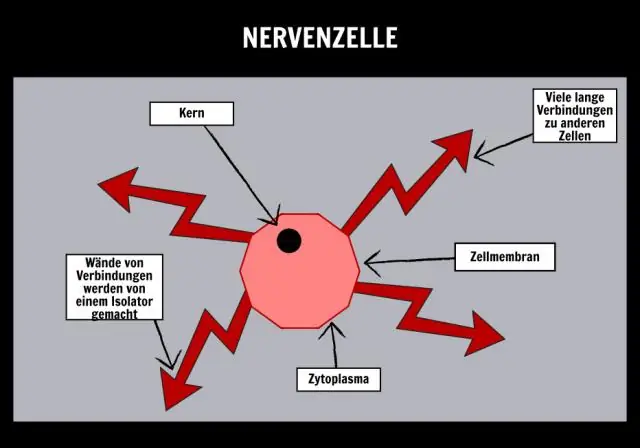
Specialiserade celler utför särskilda funktioner, såsom fotosyntes och energiomvandling. upp av cytoplasma som är omgiven av ett cellmembran och utför de grundläggande livsprocesserna. och organell i en cell utför vissa processer, såsom att tillverka eller lagra ämnen, som hjälper cellen att hålla sig vid liv
Varför behöver alla celler utföra proteinsyntes?
Proteinsyntes är den process som alla celler använder för att tillverka proteiner, som är ansvariga för all cellstruktur och funktion. Ribosomen, som är ett fack i cellen som krävs för proteinsyntes, säger åt tRNA att få aminosyror, som är byggstenarna i proteiner
Vad används icke-linjär regression till?
Icke-linjär regression är en form av regressionsanalys där data anpassas till en modell och sedan uttrycks som en matematisk funktion. Icke-linjär regression använder logaritmiska funktioner, trigonometriska funktioner, exponentialfunktioner, potensfunktioner, Lorenzkurvor, Gaussfunktioner och andra anpassningsmetoder