Video: Är en matris lik sin invers?
2024 Författare: Miles Stephen | [email protected]. Senast ändrad: 2023-12-15 23:41
Tänk bara på en 2x2 matris det är liknar dess invers utan att de diagonala posterna är 1 eller -1. Diagonal matriser ska göra. Alltså A och omvänd av A är liknande , så deras egenvärden är desamma. om ett av A:s egenvärden är n, ett egenvärde på dess omvända blir 1/n.
Frågade också, liknar en matris sin transponering?
Vilken ruta som helst matris över ett fält är liknar dess omvandling och alla kvadratiska komplex matris är liknande till ett symmetriskt komplex matris.
Likaså, är alla inverterbara matriser lika? Om A och B är det liknande och inverterbar , då är A–1 och B–1 liknande . Bevis. Eftersom Allt de matriser är inverterbar , vi kan ta inversen av båda sidorna: B–1 = (P–1AP)–1 = P–1A–1(P–1)–1 = P–1A–1P, så A–1 och B–1 är liknande . Om A och B är det liknande , så är Ak och Bk för alla k = 1, 2,.
Angående detta, kan en matris likna sig själv?
Det vill säga Any matris är liknar sig själv : I−1AI=A. Om A är liknande till B, då är B liknande till A: om B=P−1AP, då A=PBP−1=(P−1)−1BP−1. Om A är liknande till B via B=P−1AP, och C är liknande till B via C=Q−1BQ, då är A liknande till C: C=Q−1P−1APQ=(PQ)−1APQ.
Vad betyder det om matriser är lika?
I linjär algebra, två n-för-n matriser A och B kallas liknande om det finns ett inverterbart n-för-n matris P sånt. Liknande matriser representerar samma linjära karta under två (eventuellt) olika baser, där P är förändringen av basen matris.
Rekommenderad:
Hur relaterar ordet matris till mitokondrier?
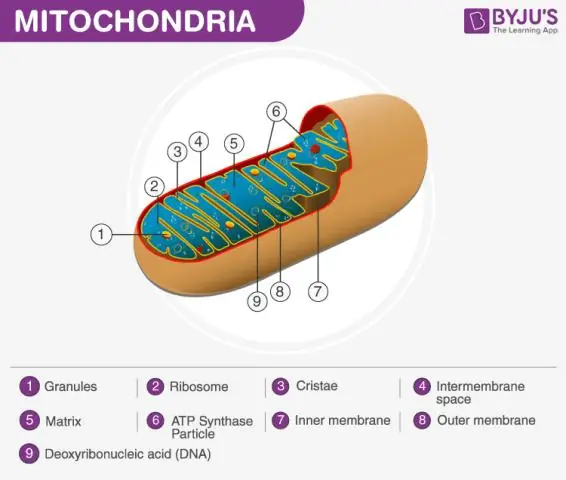
Mitokondriematrisen definierad Mitokondrien består av ett yttre membran, ett inre membran och ett gelliknande material som kallas matrisen. Denna matris är mer trögflytande än cellens cytoplasma eftersom den innehåller mindre vatten. Detta är ett viktigt steg i cellandningen, som producerar energimolekyler som kallas ATP
Hur roterar man en 45 graders matris?
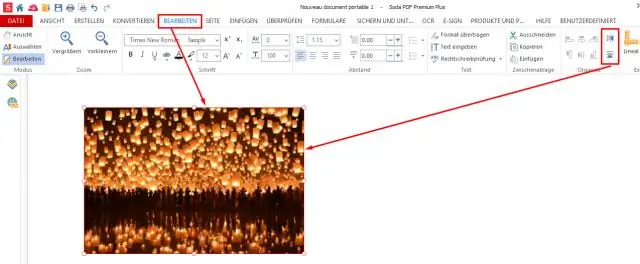
Formeln för denna rotation är: RM[x + y - 1][n - x + y] = M[x][y], där RM betyder roterad matris, M den initiala matrisen och n dimensionen för den initiala matrisen (som är nxn). Så, a32, kommer från den tredje raden och den andra kolumnen till den fjärde raden och den fjärde kolumnen
Vilken reaktion sker i mitokondriernas matris?
Mitokondriematrisen definierad Det är där citronsyracykeln äger rum. Detta är ett viktigt steg i cellandningen, som producerar energimolekyler som kallas ATP. Den innehåller mitokondrie-DNA i en struktur som kallas en nukleoid
Hur gör man en matris till en identitetsmatris?
VIDEO Dessutom, hur hittar du inversen av en matris med hjälp av en identitetsmatris? Det fungerar på samma sätt för matriser . Om du multiplicerar a matris (som A) och dess omvänd (i det här fallet A – 1 ), får du identitetsmatris I.
Hur hittar man den additiva inversen av en matris?
För att få additiv invers av given matris behöver vi bara multiplicera varje element i matrisen med -1. När vi multiplicerar varje element i matrisen med -1, blir det lika med -A. Därför blir A+(-A) lika med 0 där 0 är en nollmatris. Den uppfyller den grundläggande definitionen av additiv invers