Video: Pendlar Hamiltonian med vinkelmoment?
2024 Författare: Miles Stephen | [email protected]. Senast ändrad: 2023-12-15 23:41
När en partikel är under påverkan av en central (symmetrisk) potential, då L pendlar med potentiell energi V(r). Om L pendlar med Hamiltonian operatör (kinetisk energi plus potentiell energi) sedan vinkelmoment och energi kan kännas samtidigt.
På detta sätt, pendlar rörelsemängd med rörelsemängd?
De vinkelmoment operatörer do inte pendla , men det är fortfarande möjligt för vinkelmoment vara noll i alla tre riktningarna. Men så snart som vinkelmoment i vilken riktning som helst är icke-noll, endast en komponent av vinkelmoment kan ha ett bestämt värde.
På samma sätt, vad är vinkelmomentum inom kvantmekaniken? De vinkelmoment operatör spelar en central roll i teorin om atomfysik och annat kvant problem som involverar roterande symmetri. Både i klassiskt land kvantmekanisk system, vinkelmoment (tillsammans med linjär Momentum och energi) är en av rörelsens tre grundläggande egenskaper.
Bara så, pendlar spinn och rörelsemängd?
jeblack3 sa: Snurra är inte vinkelmoment av en partikel. Det totala vinkelmoment av aparticle är snurra plus orbital vinkelmoment . Theorbital komponent gör det inte pendla med Momentum , men snurra komponent gör.
Är rörelsemängdsoperatorn hermitisk?
Angular Momentum Operators . Dessutom med tanke på att det och de finns Hermitiska operatörer , det är lätt att se att de också är Hermitian . Detta är viktigt, eftersom endast Hermitiska operatörer kan representera fysiska variabler inkvantmekanik (se avsnitt 4.6).
Rekommenderad:
Kan föräldrar med blodgrupp A och B få ett barn med O?
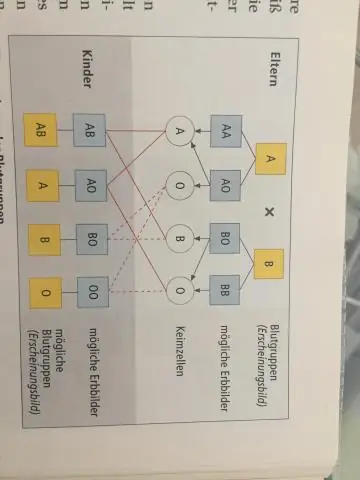
Ja, eftersom varje person har två "gener" för blodgrupp. Två föräldrar med A- eller B-blodgrupp kan därför producera ett barn med blodgrupp O. Om de båda har AO- eller BO-generna kan varje förälder donera en O-gen till avkomman. Avkomman skulle då ha OO-gener, vilket gör dem till blodgrupp O
Vad är syftet med kyvetten med endast referensmaterial?
En tom kyvett används för att kalibrera spektrofotometeravläsningarna: de dokumenterar baslinjesvaret för miljö-instrument-provsystemet. Det är analogt med att "nolla" en våg innan vägning
Vad är en fördel med kalibrering med standardtillägg?
Fördelarna med standardadditionsmetoden är mycket användbara när provsammansättningen är okänd eller komplex och påverkar analytsignalen och är bekväm för volumetriska och kromatografiska analyser
Är reaktor med packad bädd och reaktor med fast bädd samma?
I fastbäddsreaktorer görs reaktionen på ytan av pelleten inuti reaktorn, och pelleten fungerar som en katalysator för reaktionen. I en reaktor med packad bädd görs reaktionen genom att finblanda de två flödena av kemikalier genom fysisk blandning
Vilka egenskaper har LET-strålningar med hög linjär energiöverföring jämfört med låg LET-strålning?
Vilka egenskaper har strålning med hög linjär energiöverföring (LET) jämfört med strålning med låg LET? Ökad massa, minskad penetration. (På grund av sin elektriska laddning och betydande massa orsakar de fler joniseringar i en tät mängd vävnad, vilket snabbt förlorar energi