
- Författare Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:40.
- Senast ändrad 2025-01-22 17:10.
Ekvipotentiallinjer vid olika potentialer kan aldrig korsa antingen. Detta beror på att de per definition är en linje med konstant potential. De ekvipotential vid en given punkt i rymden kan bara ha ett enda värde. Obs: Det är det möjligt för två rader representerar samma potential att korsa.
Kan två ekvipotentiella ytor skära varandra på motsvarande sätt ge skäl?
Nej det kan de inte skära varandra eftersom två olika ekvipotentialer yta har annorlunda elektrisk potential, så om de korsas då poängen med korsning kommer ha två olika potentialer vid samma punkt vilket inte är möjligt.
Vid sidan av ovan, varför är ekvipotentiallinjerna nära ledarytor parallella med ytan? Så anledningen varför ekvipotentiallinjer är parallellt med ytan beror på att eftersom det finns elektriska fält som rör vid yta , sedan ekvipotentiallinjer kommer vara parallell till de elektriska fälten och parallell till ledarens yta.
Med tanke på detta, såg du någonsin två E-fältlinjer korsa. Vad sägs om två ekvipotentialer Varför eller varför inte?
Det är inte möjligt för två annorlunda ekvipotentiallinjer eller två elektriska tvinga rader till korsa eftersom ekvipotentiallinjer har fasta värden per definition. Om de var till korsa sedan det skulle skapa två olika värderingar vilket är meningslöst.
Hur är elektriska fältlinjer relaterade till ekvipotentiallinjer Hur korsar de varandra?
Elektriska fältlinjer från en viss källa avgift alltid korsa detta ekvipotential yta vinkelrät mot denna yta. Så om du har en positiv punktladdning, där elektriska fältlinjer strålar utåt, de ekvipotential ytan runt denna punkt är laddningen sfärisk.
Rekommenderad:
Är det möjligt för två ekvipotentiallinjer att korsa två elektriska fältlinjer förklara?

Ekvipotentiallinjer vid olika potentialer kan heller aldrig korsas. Detta beror på att de per definition är en linje med konstant potential. Potentialekvivalenten vid en given punkt i rymden kan bara ha ett enda värde. Obs: Det är möjligt för två linjer som representerar samma potential att korsa
Hur gör cellstrukturer det möjligt för en cell att utföra grundläggande livsprocesser?
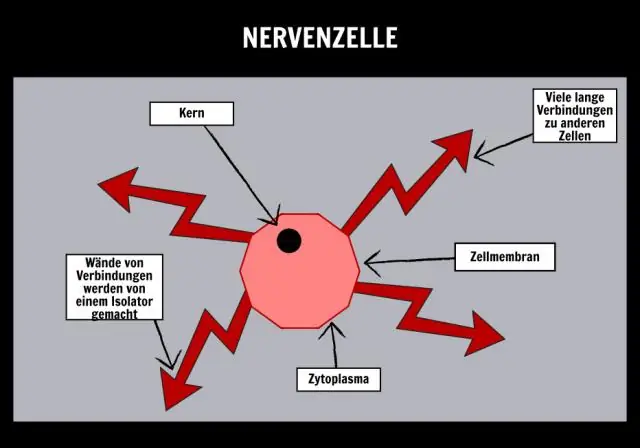
Specialiserade celler utför särskilda funktioner, såsom fotosyntes och energiomvandling. upp av cytoplasma som är omgiven av ett cellmembran och utför de grundläggande livsprocesserna. och organell i en cell utför vissa processer, såsom att tillverka eller lagra ämnen, som hjälper cellen att hålla sig vid liv
Vad är förhållandet mellan elektriska fältlinjer och ekvipotentiella ytor?

Ekvipotentiallinjer är alltid vinkelräta mot det elektriska fältet. I tre dimensioner bildar linjerna ekvipotentiella ytor. Rörelse längs en ekvipotentiell yta kräver inget arbete eftersom sådan rörelse alltid är vinkelrät mot det elektriska fältet
Är det möjligt för ett system med två linjära ekvationer att inte ha någon lösning som förklarar ditt resonemang?

System med linjära ekvationer kan bara ha 0, 1 eller ett oändligt antal lösningar. Dessa två linjer kan inte skära varandra två gånger. Det korrekta svaret är att systemet har en lösning. Totalt antal poäng Antal 2-punktskorgar Antal 3-punktskorgar 17 4 (8 poäng) 3 (9 poäng) 17 1 (2 poäng) 5 (15 poäng)
Varför är elektriska fältlinjer vinkelräta mot ekvipotentiella ytor?

Eftersom de elektriska fältlinjerna pekar radiellt bort från laddningen är de vinkelräta mot ekvipotentiallinjerna. Potentialen är densamma längs varje ekvipotentiallinje, vilket innebär att inget arbete krävs för att flytta en laddning någonstans längs en av dessa linjer
