
Innehållsförteckning:
- Författare Miles Stephen [email protected].
- Public 2023-12-15 23:40.
- Senast ändrad 2025-06-01 05:06.
Omvänd av icke-konstant Linjära funktioner . A linjär funktion kommer att vara inverterbar så länge den är icke-konstant, eller med andra ord har lutning som inte är noll. Du kan hitta omvänd antingen algebraiskt eller grafiskt genom att reflektera den ursprungliga linjen över diagonalen y = x.
På samma sätt, har linjära funktioner alltid en invers?
2 svar. Kännetecknande för icke-vertikala "räta linjer" är att de överensstämmer med funktioner som kan föreskrivas av x↦ax+b där a, b är fasta reella tal. Detta säger oss att sådana linjära funktioner har en invers om a≠0. I fallet a=0 har vi att göra med en konstant fungera föreskrivs av x↦b.
Dessutom, är en linjär funktion inverterbar? Den allmänna formen av en inverterbar , linjär funktion är (y=ax+q enspace (a e 0)) och dess omvänd är (y=frac{1}{a}x-frac{q}{a}).
Hur kan du sedan avgöra om en invers existerar givet en linjär funktion?
Viktiga steg för att hitta inversen av en linjär funktion
- Ersätt f(x) med y.
- Byt rollerna för "x" och "y", med andra ord, byta x och y i ekvationen.
- Lös för y i termer av x.
- Ersätt y med f −1(x) för att få den inversa funktionen.
Hur avgör man om en funktion har en invers?
Exempel 5: Om f(x) = 2x - 5, hitta omvänd . Detta fungera passerar den horisontella linjen Testa vilket betyder att det är en onetoone fungera den där har en invers . y = 2x - 5 Ändra f(x) till y. x = 2y - 5 Byt x och y.
Rekommenderad:
Hur är lösningen av linjära olikheter och linjära ekvationer lika?

Att lösa linjära olikheter är mycket likt att lösa linjära ekvationer. Den största skillnaden är att du vänder på olikhetstecknet när du dividerar eller multiplicerar med ett negativt tal. Att plotta linjära ojämlikheter har några fler skillnader. Den del som är skuggad inkluderar värden där den linjära olikheten är sann
Varför kallas trigonometriska funktioner cirkulära funktioner?

Trigonometriska funktioner kallas ibland cirkulära funktioner. Detta beror på att de två grundläggande trigonometriska funktionerna – sinus och cosinus – definieras som koordinaterna för en punkt P som färdas runt på enhetscirkeln med radie 1. Sinus och cosinus upprepar sina utgångar med jämna mellanrum
Hur transformerar man linjära funktioner?
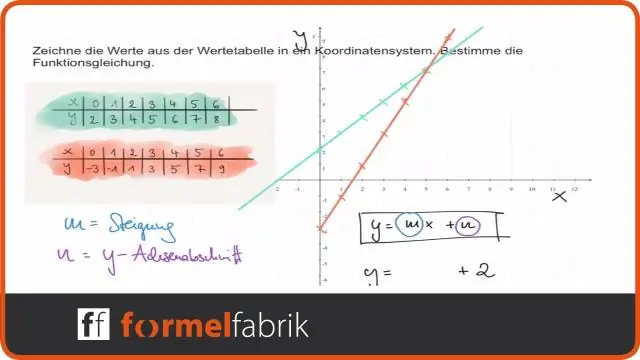
Så här gör du: Med tanke på ekvationen för en linjär funktion, använd transformationer för att plotta den linjära funktionen i formen f(x)=mx+b f (x) = m x + b. Graf f(x)=x f (x) = x. Dra ut eller komprimera grafen vertikalt med en faktor |m|. Flytta grafen uppåt eller nedåt b enheter
Vad är syftet med linjära funktioner?
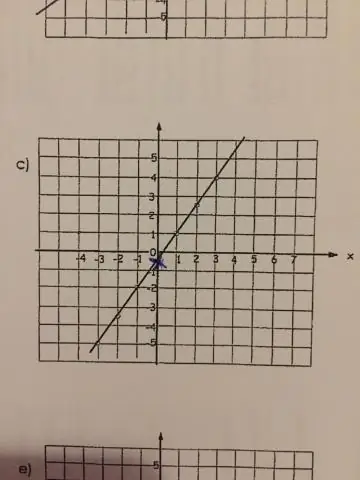
En linjär funktion är vilken funktion som helst som plottar till en rät linje. Vad detta betyder matematiskt är att funktionen har antingen en eller två variabler utan exponenter eller potenser. Om funktionen har fler variabler måste variablerna vara konstanter eller kända variabler för att funktionen ska förbli en linjär funktion
Vilka är några verkliga exempel på linjära funktioner?

Ursprungligen besvarade: Kan någon ge mig ett exempel på en situation med linjära funktioner i verkligheten? Linjära funktioner inträffar när du har en konstant förändringshastighet. Verkliga exempel är: Hitta ström som förbrukats dag 1,2,3… Du hyr en bil. Du kör bil i en hastighet av 60 km/h
