2025 Författare: Miles Stephen | [email protected]. Senast ändrad: 2025-01-22 17:10
Riktningen är linjen y = k - p. Axeln är linjen x = h. Om p > 0, parabel öppnas uppåt, och om p < 0, parabel öppnas nedåt. Om en parabel har en horisontell axel, standardformen för ekvationen av parabel är detta: (y - k)2 = 4p(x - h), där p≠ 0.
Dessutom, vad är en konisk sektionsparabel?
< Koniska sektioner . De parabel är en annan allmänt känd konisk sektion . Den geometriska definitionen av a parabel är platsen för alla punkter så att de är på samma avstånd från en punkt, känd som fokus, och en rät linje, som kallas riktlinjen. Med andra ord excentriciteten hos en parabel är lika med 1.
För det andra, hur identifierar man en konisk? Om de är det, är dessa egenskaper följande:
- Cirkel. När x och y båda är kvadratiska och koefficienterna på dem är desamma - inklusive tecknet.
- Parabel. När antingen x eller y är kvadratisk - inte båda.
- Ellips. När x och y båda är kvadratiska och koefficienterna är positiva men olika.
- Hyperbel.
Också att veta är, vad är ekvationen för parabel?
Givet fokus (h, k) och riktningen y=mx+b, är ekvation för en parabel är (y - mx - b)^2 / (m^2 +1) = (x - h)^2 + (y - k)^2.
Hur bildas parabel?
A parabel är kurvan bildas genom skärningspunkten mellan ett plan och en kon, när planet är i samma lutning som sidan av konen.
Rekommenderad:
Hur ritar man ett absolut värde på en TI 84 Plus?
Exempel 1: Lös: Ange vänster sida i Y1. Du kan snabbt hitta abs() under CATALOG (över 0) (eller MATH → NUM, #1 abs() Ange höger sida i Y2. Använd alternativet Intersect (2:a CALC #5) för att hitta var graferna skär varandra. Flytta spindel nära skärningspunkten, tryck ENTER Svar: x = 4, x = -4
Hur ritar man en hyperbolisk funktion?
Grafer över hyperboliska funktioner sinh(x) = (e x - e -x)/2. cosh(x) = (e x + e -x)/2. tanh(x) = sinh(x) / cosh(x) = (ex - e -x) / (ex + e -x) coth(x) = cosh(x) / sinh(x) = (ex + e - x) / (ex - e -x) sech(x) = 1 / cosh(x) = 2 / (ex + e -x) csch(x) = 1 / sinh(x) = 2 / (ex - e - x)
Hur ritar man ett frikroppsdiagram?
För att rita ett frikroppsdiagram, ritar vi objektet av intresse, ritar alla krafter som verkar på objektet och löser upp alla kraftvektorer till x– och y-komponenter. Vi måste rita ett separat frikroppsdiagram för varje objekt i problemet
Hur hittar man spetsen på en horisontell parabel?
Om en parabel har en horisontell axel är standardformen för parabelns ekvation denna: (y -k)2 = 4p(x - h), där p≠ 0. Spetsen på denna parabel är vid (h, k). Fokus är på (h + p, k). Thedirectrix är linjen x = h - p
Hur gör man en konisk sektion av en parabel?
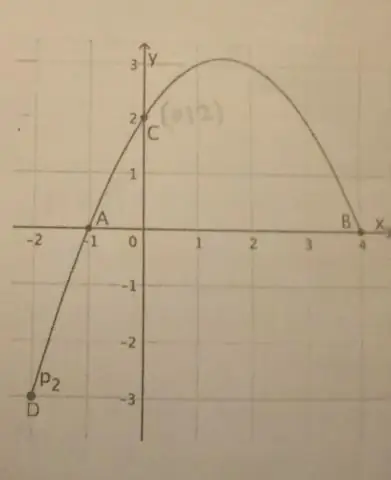
Om en parabel har en vertikal axel, är standardformen för parabelns ekvation denna: (x - h)2 = 4p(y - k), där p≠ 0. Spetsen för denna parabel är vid (h, k). Fokus är på (h, k + p). Riktningen är linjen y = k - p